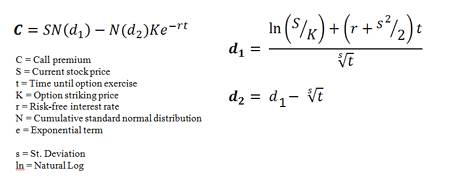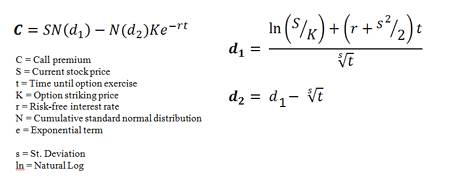adibool a écrit :C'est pour cela qu'on a tant de mal à pricer les options IG . Le "smile" de volatilité n'en ai pas vraiment un .
Quel programme Python utilises tu ? Home made ou internet?
Ca serait intéressant de reporter le graphique a différent moment pour voir si le "smile" change de forme.
J'utlise un petit scipt fait maison:
Code : #
import numpy as np
# Strike
K = np.ar ([12020, 12040, 12060, 12080, 12100, 12120, 12130, 12140, 12150, 12160, 12170, 12180, 12190, 12200, 12220, 12240, 12260, 12280, 12300])
# Pris du call correspondant (bid+ask / 2)
p_call = np.ar ([105.6, 85.6, 65.7, 46.1, 28.2, 13.9, 8.7, 5.2, 19.1, 26.7, 35.3, 44.5, 54.1, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5] )
S0 = 12125.6 # cours actuel
r = 0.0 # taux d'interet
t = 1./365 # temps avant l'echeance
div = 0 # dividende
Vol = [] # Vol implicite
# On teste toutes les valeurs de 0 a 100% avec un pas de 1
# On garde celle qui minimise l'ecart entre le prix reel et le prix de IG
for i, c in enumerate(p_call):
X = np.arange(0., 1., 0.01)
Y = [ abs(call(S0, K[i], v, r, t, div) - c) for v in X]
Vol += [np.argmin(Y)]
# tracer
import matplotlib.pyplot as plt
plt.plot(K, Vol, 'ro-')
plt.show()
La fonction call est presente dans le fichier blackscholes.py que j'ai récupérer sur internet (la flemme de retaper la formule)
Code : #
import scipy
import math
from scipy import stats
""" Price an option using the Black-Scholes model.
s: initial stock price
k: strike price
t: expiration time
v: volatility
r: risk-free rate
div: dividend
cp: +1/-1 for call/put
"""
d1 = lambda s,k,v,r,t,div : (scipy.log(s/k)+(r-div+0.5*math.pow(v,2))*t)/(v*scipy.sqrt(t))
d2 = lambda s,k,v,r,t,div : d1(s,k,v,r,t,div) - v*scipy.sqrt(t)
call = lambda s,k,v,r,t,div : (s*math.exp(-div*t)*stats.norm.cdf(d1(s,k,v,r,t,div))) - (k*scipy.exp(-r*t)*stats.norm.cdf(d2(s,k,v,r,t,div)))
Je vais essayer de récupérer les cotes pour d'autres périodes pour voir si ça change. (Ceci dit, vous connaisez une méthode pour récupérer les prix de IG sous forme texte sans avoir a les rentrer un à un comme je l'ai fait ici? )
Bella Swan a écrit :maroxe a écrit :Je n'arrive pas à expliquer la forme de cette courbe, tout indice est le bienvenu.
J'utilise le modèle de BlackScholes classique,
Les travaux de Peter Tankov ?
C'est possible, c'était mon prof de TD, mais il a jamais dit que le modèle était basé sur ses travaux.
Ceci dit, le modèle est simple pour les options vanilles comme ici, comme les options call européennes ont le même prix que les américaines, le prix est donné par:
D'ailleurs, j'essaye de retrouver ce que j'ai appris dans son cours dans la vrai vie sans grand succès pour l'instant 
