Le principe de diversification en gestion de portefeuille

Les travaux de Harry Markowitz ont en partie abouti à la conclusion que la diversification permet une réduction du niveau de risque dans le cadre de la constitution d'un portefeuille boursier.
En effet, Markowitz a établi le fait qu'en diversifiant son portefeuille, on réduit le risque de celui-ci, tout en gardant un rendement satisfaisant. Il conseille l'utilisation de tous les types d'actifs pour une diversification parfaite.
Exemple de diversification en gestion de portefeuille
| Situation possible | Probabilité | Rendement de l'action A | Rendement de l'action B |
| 1 | 20% | 5% | 50% |
| 2 | 30% | 10% | 30% |
| 3 | 30% | 15% | 10% |
| 4 | 20% | 20% | -10% |
| Rendement espéré | ------------ | 12,5% | 20% |
Le rendement espéré se calcule en faisant une moyenne pondérée des rendements de chaque action.
Nous allons donc premièrement calculer le risque de chaque action, de façon indépendante. Pour cela, on calcule d'abord la variance des deux actions. La déviation standard, ce qui équivaut au risque, se trouve en faisant la racine carrée de la variance.
Variance A = 20% (5%-12,5%)²+30%(10%-12,5%)²+30%(15%-12,5%)²+20%(20%-12,5%)²
Variance A = 0,00263
Standard Déviation (STD) = √Variance
Standard Déviation = 5,12%
Variance B = 0,042
Standard Déviation B = 20,49%
Création d'un portefeuille avec les actions A ET B:
Nous allons associer les deux actions dans un portefeuille, en plaçant 50% de nos fonds sur chacune des 2 actions.
Le retour espéré devient alors = 50% x 12,5% + 50% x 20% = 16,25%
Il faut ensuite calculer la covariance entre tous les actifs du portefeuille, en l'occurrence entre nos deux actions. La covariance donne la possibilité d’évaluer les variations simultanées de deux variables en fonction de leur moyenne respective.
Covariance = 20% (5%-12,5%)(50%-20%) + 30% (10%-12,5%)(30%-20%) + 30% (15%-12,5%)(10%-20%) + 20% (20%-12,5%)(-10%-20%).
Covariance = -0,0105
Risque du portefeuille:
Risque du portefeuille = (50%² x 5,12%²) + (50%² x 20,49%²) + 2(50% x 50% x -0,0105) = 0,00591
Risque du portefeuille = Standard déviation
Standard déviation = √0,00591
Standard déviation = 7,69%
On remarque donc que l'association permet d'obtenir un rendement espéré de 16,25% pour un niveau de risque de 7,69%. Ce qui optimise les deux actions de base qui proposaient une STD de 5,12% associé à un rendement espéré de 12,5% pour l'action A et une STD de 20,49% associé à un rendement espéré de 20% pour l'action B.
Les risques systématiques et non systématiques
La diversification du portefeuille ne permet pas de réduire tout le risque. Il y a en effet deux types de risques: Le risque systématique et le risque non systématique. Un portefeuille bien diversifié permet de réduire le risque non systématique mais la diversification ne permet pas de réduire le risque systémique, qui correspond au risque du marché.
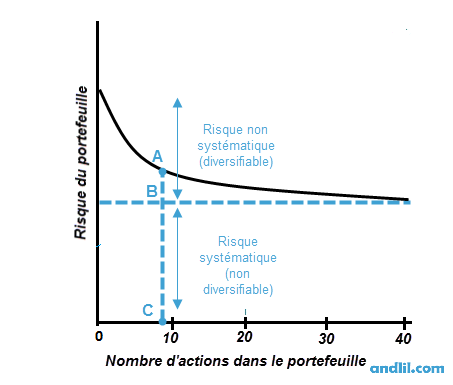
Plus un portefeuille est diversifié, plus le risque non systématique est réduit. Le risque systématique reste lui inchangé.
Ce schéma illustre le processus de réduction du risque non systématique par la diversification. Le risque total est représenté par le segment AC. Plus le nombre d'action dans le portefeuille augmente, plus le risque non systématique, représenté par AB, est faible. BC, représentant le risque systématique, ne réduit pas via le processus de diversification.
Le guide théorique de la gestion de portefeuille :
- Le principe de diversification en gestion de portefeuille
- Le portefeuille efficient selon Markowitz
- Théorie du marché de capitaux
- L'introduction du Coefficient Bêta
Auteur de l'article :Benoist Rousseau est diplômé de l'université Paris-Sorbonne en histoire économique contemporaine et de la Certification Professionnelle des Acteurs des Marchés Financiers de l'AMF. Il a été professeur d'histoire pendant 12 ans avant de devenir trader en compte propre. Ancien Conseiller en Investissements Financiers, il est aussi écrivain. Son ouvrage "Devenez Trader Pro" est numéro 1 des ventes dans la catégorie bourse depuis de nombreux mois. Intervenant régulier sur TV Finance et divers médias, il est suivi par plus de 150.000 personnes sur les réseaux sociaux.
Laisser un commentaire
Avertissement : La négociation sur instruments financiers à effet de levier peut vous exposer à des risques de pertes supérieures aux dépôts et ne convient qu'à une clientèle avisée ayant les moyens financiers de supporter un tel risque. Les transactions sur instruments de change (forex) et contrats sur différence (CFD) sont hautement spéculatives et particulièrement complexes et s’accompagnent d’un niveau de risque élevé en raison de l’effet de levier. Vous devez vous assurer que vous comprenez comment ces instruments fonctionnent et que vous pouvez vous permettre de prendre le risque élevé de perdre votre argent. Les vidéos et les articles de ce site n’ont qu’une portée pédagogique et informative, ce ne sont pas des conseils en investissement ni une incitation quelconque à acheter ou vendre des instruments financiers. Tout investisseur doit se faire son propre jugement avant d'investir dans un produit financier afin qu'il soit adapté à sa situation financière, fiscale et légale.

4 Commentaires pour Le principe de diversification en gestion de portefeuille
Nice maths, very nice when applied to physics. But not great for stocks which behave outside the frame of that theory. Why? Because volatility is not a constant and that makes all the difference! Moreover, what about increased correlations when the market falls sharply? In my opinion, too much diversification will begin at a time to seriously damage your performance, especilally if you are a good stock-picker.
These are theoretical works that have no purpose to optimize the return on investment but reduce risk. By reducing the risk, long-term gains is increased.
salut!
c'est super intéressant car ici au lieu de calculer la variance et l'écart-type sur une succession de périodes, on l'a calculé en faisant intervenir la probabilité du rendement correspondant. Déjà cela sous-entend que l'on parle de rendements sur une seule et même période et que l'on connaisse la probabilité de ces rendements.
Pour moi l'écart type est :
(Somme de n(rendement-rendement moyen)²) / nombre de périodes n
je ne comprend pas pourquoi dans les calculs de variance tu multiplies par les probabilités chaque élément de la somme au lieu de diviser à la fin toutes les sommes par 4 (cad le nombre de périodes)....
L'auteur multiplie par la probabilité car la formule de la Variance probabilisée utilisée ici fonctionne de cette façon. Elle est égale à la somme des calculs suivants : probabilités de l'action concernée x (le rendement de la situation x - le rendement moyen de l'action concernée) au carré.
Et l'écart type est la racine carrée de la variance puisque par définition il s'agit de connaître en moyenne, de combien les valeurs sont écartées de la moyenne.