Théorie du marché des capitaux

Présentation de la théorie du marché des capitaux

La théorie du marché des capitaux (Capital Market theory) est une extension de la théorie moderne du portefeuille d'Harry Markowitz. Elle émet des hypothèses sur le comportement des investisseurs, là où la théorie moderne du portefeuille définit comment les investisseurs devraient agir.

Le MEDAF (modèle d'évaluation des actifs financiers), introduit principalement par Sharpe en 1964 est une mise en application de la théorie du marché des capitaux. C'est un modèle qui évalue le risque d'un actif.

Les postulats de la théorie du marché des capitaux

Cette théorie repose sur différentes hypothèses :

• Tous les investisseurs peuvent emprunter et prêter au taux sans risque.
• Tous les investisseurs utilisent la théorie moderne du portefeuille et ont les même données de calcul : ils attribuent la même variance, et le même rendement espéré pour tous les actifs. Pour un nombre donné d'actif, les investisseurs, ayant les mêmes informations ont une frontière efficiente identique.
• Les investisseurs se positionnent sur la même période de temps unique.
• Il n'y a pas de coût de transaction
• Il n'y a pas de taxe sur les plus-values
• Il n'y a pas d'inflation
• Aucun acteur ne peut influencer le marché par une de ses prises de position sur ce dernier
• Les marchés sont à l'équilibre

Ces hypothèses peuvent paraître irréalistes au premier abord mais l'importance réside plus dans la qualité de la description de la réalité grâce à ce modèle, plutôt que la réalité des hypothèses elles-mêmes. L'influence de ces hypothèses sur la qualité finale de l'information apportée par ce modèle est trop faible pour pouvoir dénigrer ce dernier. Les coûts de transaction sont trop faibles pour vraiment influencer l'information apportée par le modèle. L'inflation peut être partiellement anticipée sur une période donnée et n'est alors plus un facteur majeur.

Qu'est ce que le taux sans risque ?

L'une des hypothèses de la théorie des marchés des capitaux est que tous les investisseurs peuvent emprunter et prêter au taux sans risque. C'est l'introduction de ces actifs sans risques qui permettent de développer cette théorie en partant de la théorie moderne du portefeuille.

Ce taux sans risque est une valeur nominale et non une valeur réelle. Un actif au taux sans risque peut être défini comme un actif au rendement espéré certains possédant une variance de rendement égale à 0. Cet actif a une covariance égale à 0 avec n'importe quel actif possédant un niveau de risque réel.

Pour mettre en pratique cette théorie, les investisseurs utilisent généralement les obligations d'État, pour lesquels il n'y a pas de risque de défaut et qui ont un rendement connu à l'avance.

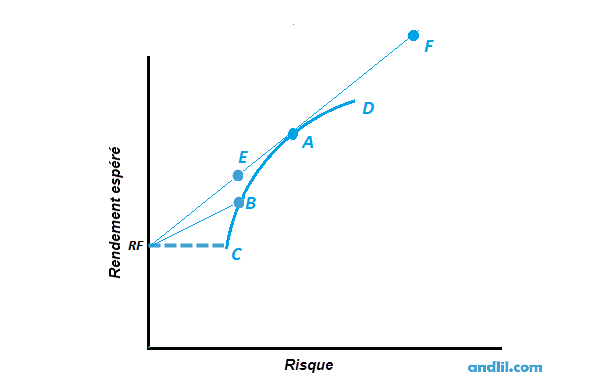
Schéma 1:Les nouvelles possibilités grâce au taux sans risque

Prêter et emprunter au taux sans risque

Partons d'une frontière efficiente définie par l'arc CD sur le schéma 1. Cette frontière définit les possibilités de portefeuilles constitués d'actions risquées sans emprunter ni prêter. Nous avons rajouté le taux sans risque (RF). Il existe maintenant de nouvelles possibilités de combinaisons d'actifs sans  risques (peu risqués) et d'actifs risqués en traçant la droite RF-A, tangente à la frontière efficiente.

Possibilités de prêts au taux sans risque

En combinant des actifs risqués à des actifs sans risques, on peut voir que des nouvelles possibilités de portefeuilles sont accessibles. Le portefeuille E, constitué d'actifs peu risqués et d'actifs risqués domine le portefeuille B (constitué uniquement d'actifs risqués) qui est situé sur la frontière efficiente. Tous les portefeuilles situés en dessous de la tangente RF-A sont dominés par ceux qui se trouvent sur cette tangente.

On parle de prêt car les portefeuilles qui s'y trouvent sont constitués d'obligations d'État peu risquées où l'investisseur se retrouve prêteur lorsqu'il les possèdent.

Possibilités d'emprunts

L'investisseur a la possibilité d'emprunter des fonds pour pouvoir augmenter sa capacité d'investissement ce qui permet d'augmenter les possibilités de constitution de portefeuilles.

Un investisseur peut en effet augmenter ses possibilités de gains en investissant plus de fonds que ce que sa capacité personnelle lui permet. Une des solutions est l'achat à effet de levier ou achat sur marge ( buying stock on margin en anglais). La théorie veut également que l'investisseur puisse emprunter au taux sans risque.

Le segment AF représente les nouvelles possibilités que possède l'investisseur pour constituer son portefeuille grâce à l'utilisation de l'emprunt. Les portefeuilles situés sur cette dernière répondent à des profils d'investisseurs agressifs, tandis que ceux sur le segment RF A sont pour des profils plus prudents.

La droite de marché de capitaux

La droite RF-A-F sur le schéma 1 est appelée droite de marché des capitaux (CML). Comme il est expliqué plus haut, un investisseur se doit de choisir un des portefeuilles situé sur cette droite puisque ces derniers dominent tous les autres disponibles. Le choix du portefeuille se fait alors en fonction de la tolérance au risque de l'investisseur.

La droite de marché des capitaux met en évidence le point d'équilibre entre le rendement espéré et le risque pour un portefeuille efficient.

Sur le schéma ci-dessous, on peut apercevoir la droite des marchés des capitaux, sans la frontière efficiente de Harry Markowitz, devenue dominée par cette nouvelle droite, tangente à cette frontière au point M.

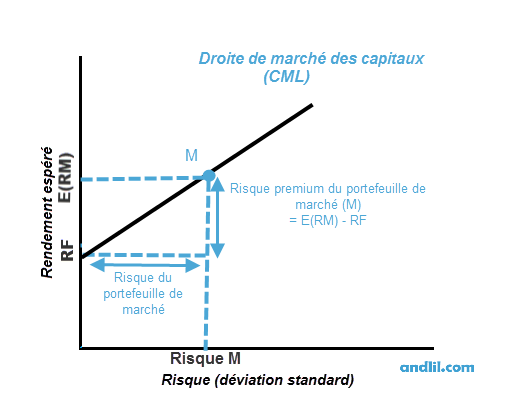
schéma 2: Droite de marché de capitaux

Le portefeuille de marché

Le point M sur le schéma 2 représente un portefeuille uniquement constitué d'actifs risqués financés à 100% par l'investisseur. On le nomme en anglais le Market portfolio (portefeuille du marché). C'est le portefeuille optimal d'actifs risqués.

En théorie, le portefeuille du marché est constitué de tous les actifs risqués du monde entier, ce qui est bien entendu impossible, mais en pratique, la diversification dans des produits étrangers est conseillée. Comme il est constitué de tous les actifs existants, sa diversification est totale et son risque est constitué uniquement du risque systématique.

L'ensemble des portefeuilles situés sur la CML sont constitués du portefeuille de marché M et d'actifs sans risque ou d'achat sur marge ( à effet de levier).

Le risque premium, spécifié sur ce schéma correspond au risque supplémentaire pris par l'investisseur, qui attend alors un rendement supplémentaire optimal pour cette prise de risque.

La distance entre la ligne horizontale partant du taux sans risque et le point M est en fait le rendement espéré supplémentaire pour récompenser la prise de risque.

On peut maintenant calculer le coefficient directeur de la droite des marchés des capitaux.

Coeff directeur CML = E(RM) - RF / risque M

A quoi correspond ce coefficient directeur ?

Le coefficient directeur de la CML correspond au prix du risque sur le marché pour les portefeuilles efficients. Il indique le rendement espéré supplémentaire accordé pour chaque pourcentage de risque supplémentaire que prend l'investisseur.

Par exemple un coefficient directeur de 0,30 indique que le marché demande ce rendement supplémentaire pour chaque % de risque supplémentaire pris.

Équation de la droite de marché de capitaux

L'équation de cette droite pour calculer le rendement espéré d'un actif quelconque situé sur la CML correspond à:

E(Rp) = RF + ((E(RM) - RF) / Risque M)) x Risque p

E(Rp) correspond au rendement espéré de n'importe quel portefeuille situé sur la CML

RF correspond au taux sans risque

E(RM) correspond au rendement espéré du portefeuille de marché

Risque M correspond à la déviation standard du portefeuille de marché

Risque p correspond à la déviation standard de portefeuille en question

Cette équation ne s'applique qu'aux portefeuilles efficients, mais afin de se rapprocher de la réalité, une nouvelle équation peut être établie pour n'importe quel actif (a)

E(Ra) = RF + E(RM) - RF / variance M x Covariance (a,M)

On voit sur cette dernière équation que le risque d'un actif peut être mesuré par sa covariance avec le portefeuille de marché.

Une mesure standardisée du risque systématique a été mise au point, il s'agit de Bêta.

Bêta est une mesure relative du risque non diversifiable d'un actif par rapport au portefeuille du marché de l'ensemble des actifs. Bêta met en relation la covariance d'un actif avec le portefeuille de marché et la variance du portefeuille de marché.

Le guide théorique de la gestion de portefeuille :

1. Le principe de diversification en gestion de portefeuille
   
2. Le portefeuille efficient selon Markowitz
3. Théorie du marché de capitaux
4. L'introduction du Coefficient Bêta